[速通笔记]2024春夏-离散数学
教师:林兰芬
TA:欧阳淑怡
知识覆盖面很广,包含了大量计算机相关的数学基础。但是因为课时不够(一学期),所以讲授的深度有些不足。基本上每节课都在哐哐推进度,如果落下一点就会补的很痛苦。平时小测错一堆/(ㄒ o ㄒ)/~~全靠期末还不错提分
这个笔记纯属期末补天所用,基本上在一个星期里写成。(凑数。。。)下面是一些更加详实的笔记
https://noughtq.github.io/notebook/math/dm/index.html
https://oneko.zone/zju/dm/#before-start
https://www.yuque.com/linguisty/zju_courses/discrete
Logic and Proofs
Propositional Equivalences
De Morgan’s Laws
proof: truth table
e.g. Translating Sentence
e.g. Logic Puzzle
e.g. fCNF and fDNF

方法一
用德摩根律和 的规则化简
然后缺少元素的化可以 disjunct 一个 或者 conjunct 来凑齐
方法二
用真值表
可以用 来简便表示
construction fDNF fCNF


e.g. 附加前提证明

Quantifiers
Equivalences

De Morgan’s law
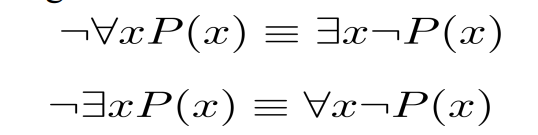
e.g. 把命题符号化
- Decide the domain of the variable
- use in and use in
e.g. Prenex normal form

- 转换成同种量词
- 进行换名(每种 x 只作用于他自己的范围,一定要换名 不要混淆哦)+辖域扩张或者用两次分配/合并
e.g. rules of inference
-
假言推理(Modus Ponens):
-
拒取推理(Modus Tollens):
-
假言三段论(Hypothetical Syllogism):
-
假言假言推理(Disjunctive Syllogism):
-
全称推理(Universal Instantiation):
-
全称引入(Universal Generalization):
-
特称推理(Existential Instantiation):
-
特称引入(Existential Generalization):
Sets
Set operations
in and not in :
universal set :
common sets :
sets can also be regarded as elements and be included in a set
empty set : note that and are different
Venn diagram
subset :
proper subset :
equal :
the size of a set : (inclusion-exclusion)
Multiset
元素可以重复出现多次
- 并集:保留元素出现个数最多的那项
- 交集:保留元素出现个数最少的那项
- 差集:元素出现个数之差,如果结果小于 0,则取 0
- 和:元素出现个数之和
Cardinality
e.g. cardinality proof (0, 1) and (a, b)
 there exists a bijection between two sets -> their cardinalities are the same
there exists a bijection between two sets -> their cardinalities are the same
- 证明 one-to-one
对于不同的不同 可以先假设相同再相减->得出的矛盾结果来证明 - 证明 onto
对于任意的值域中的值都能找到一个定义域的值
e.g. is countable infinite
- 该函数是双射函数
- 所以和此集合有相同的基数->可数无限
Power set
the set of all subsets of a set
Cartesian product
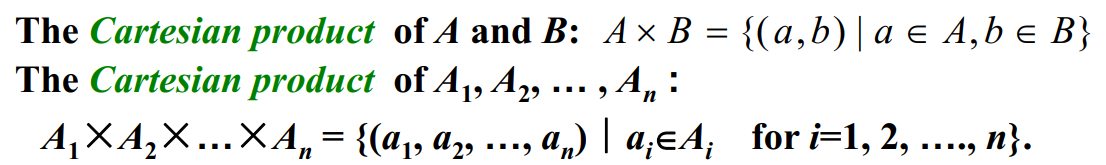
Countable and Uncountable
Countable Sets
如果一个集合:
- 是有限集
- 或者,与正整数集有相同的基数的无限集
e.g. Hilbert’s Grand Hotel
- room number: n -> n+1(1 new guest)
- room number: n -> 2n(infinite new guests)
- room number: n -> 2n then
e.g. Integers

Rational numbers

e.g. string

e.g. (0, 1) is uncountable -> the set of real number is uncountable

Functions
e.g. 证明 on-to-one/onto/bijection
- 证明 one-to-one
对于不同的不同 - 证明 onto
对于任意的值域中的值 都能找到一个定义域的值
Floor and Ceiling Functions
Properties

e.g. proof of floor and ceiling func
- Let where is an integer
- Classification discussion.
Number theory
Division
算数模
如果把算术运算限定在 可以得到算数模
即结果不会超过 m-1
Greatest Common Divisors
The Euclidean Algorithm

BEZOUT’S THEOREM
for any two nonzero integers 𝑎 and 𝑏, there exist integers 𝑥 and 𝑦 such that 𝑎𝑥+𝑏𝑦=gcd(𝑎,𝑏)
将两个数的最大公约数表示为两个数的线性组合(linear combination)
通过把执行欧几里得算法过程中的中间量反向代换
Linear Congruences
解为所有满足线性同余关系的x
e.g. 求解
- 先求出 a 的逆
- 再在式子两边同时乘上 a 的逆
- 得到仅剩的 x 同余式 所有 x 即为线性同余关系的解
Inverse
求逆
- 当 𝑚 较小时,采用观察法(暴力算法)
- 高效的做法:由已知得 gcd(𝑎,𝑚)=1,逆转欧几里得算法的步骤,得到最大公约数的线性组合表示,即 𝑠𝑎+𝑡𝑚=1,则 𝑠𝑎+𝑡𝑚≡1(mod 𝑚)。因为 𝑡𝑚 𝑚𝑜𝑑 𝑚=0,所以 𝑠𝑎≡1(mod 𝑚),因此 𝑠 即为 𝑎 模 𝑚 的逆。
The Chinese Remainder Theorem
设 是两两互素的正整数,并且 是任意整数,则存在一个整数 ,使得:
- 计算 。
- 对于每一个 ,计算 。
- 计算 在模 意义下的逆元 ,即满足 的整数 。
- 解 可以表示为:
Induction and Recursion
数学归纳法、良序性、强归纳法三者等价 可以互相证明
Mathematical Induction
数学归纳法的合法性可以用良序性证明
Strong Induction
- 基步:证明命题对初始值(通常是 0 或 1)成立。
- 归纳步:假设命题对所有小于等于某个自然数 𝑛 的值都成立,证明命题对 𝑛+1 也成立。
e.g.

Recursion
集合、字符串、位串、合式公式都可以通过递归定义:包含
- basic step
- recursive step
Structural Induction
e.g. 证明字符串长度的递归定义

Generalized Induction
在整数集以外,其他具有良序集的集合同样可以用广义数学归纳法 比如字典序的集合中
e.g.

Counting
Basic rules
Product rule
e.g. counting functions
How many functions from a set with m elements to a set with n elements
How many one-to-one functions?
e.g. counting subsets
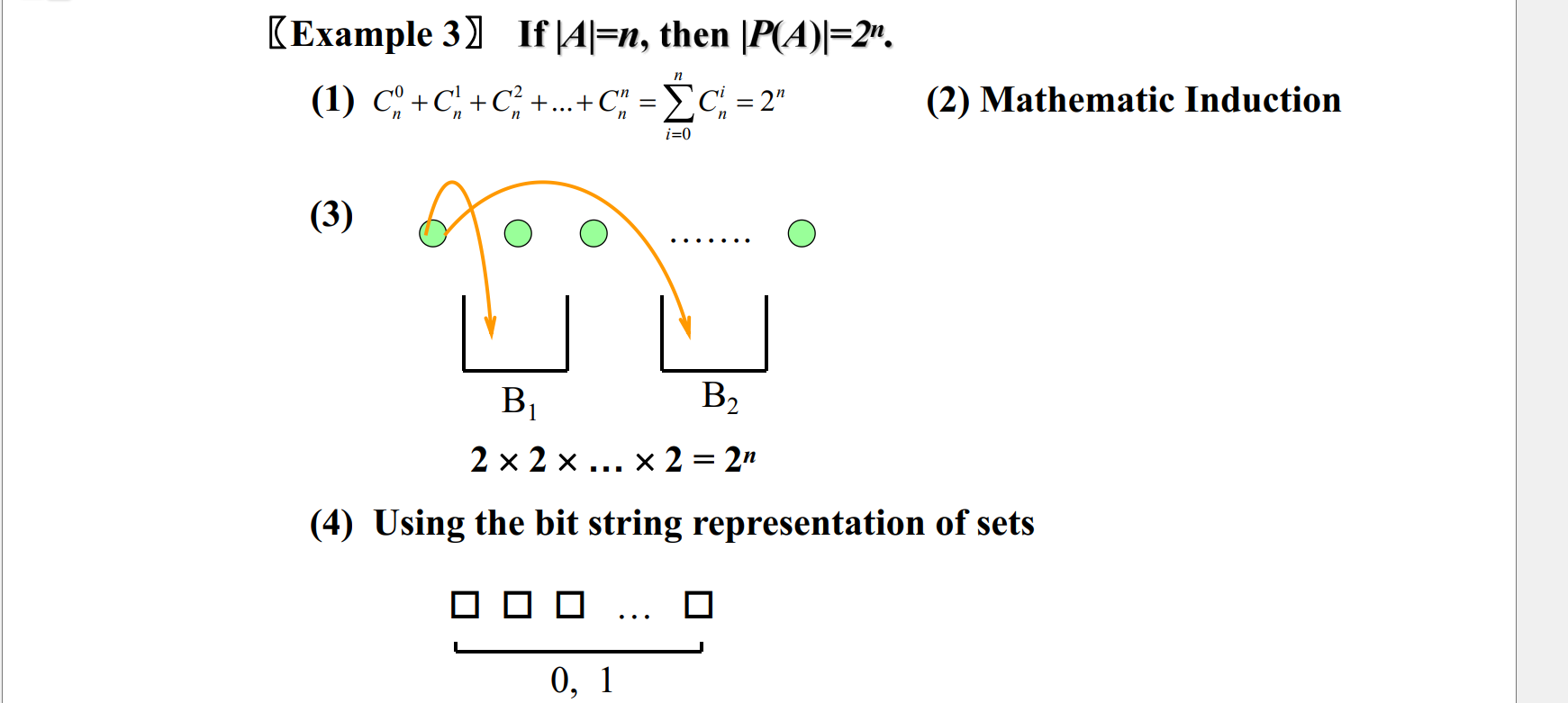
Subtraction rule
Sum rule
Pigeonhole rule
e.g.

Generalized pigeonhole rule
N objects are allocated in to k boxes at least one box containing at least objects
e.g.


Permutation and Combination
Combination corollary
1.Pascal’s identity:
2.Binomial Theorem
3.Vandermonde’s identity
combinatorial proof
- double counting proof
- bijective proof
e.g.

Permutation with Repetition
定理 1:对包含 𝑛 类对象的集合进行 𝑟 排列,如果允许重复,则总数为
Combination with Repetition
定理 2:对包含 𝑛 类对象的集合进行k组合,如果允许重复,则总数为
e.g. number of solutions to the equation

Permutation with Indistinguishable Objects
e.g. 对一个字符串进行重排

Distinguishable Objects and Distinguishable Boxes
与以上的情况一致 相当于每个箱子都是不一样的
e.g. 四个人各抓五张牌的情况数 (5 boxes 52 objects)

Indistinguishable Objects and Distinguishable Boxes
与可重复 n 类进行 k 组合的情况一致
Distinguishable Objects and Indistinguishable Boxes
第二类斯特林数 将 n 个可区分的物品放入 k 个不可区分的盒子中
如果要求每个箱子非空的话:方法数为
如果箱子可以为空 那就要把 1~k 所有斯特林数加起来才得到方法数
Indistinguishable Objects and Indistinguishable Boxes
没有闭合公式可以解决这个问题
只能转化成:求解至多k个非递增顺序排列的整数(boxes)之和等于n(objects)的情况数
e.g. 进行枚举

Solving Linear Recurrence Relations
k阶常系数线性齐次递推关系
以二阶为例
把
得到其特征方程为
- 没有重根 解为:
- 有重根的时候 解为:
常数通过给出的基础步骤解方程得出
常系数线性非齐次递推关系
1.找到关联的线性齐次递推关系 并得出特征根以及解 2.
e.g. 的解

Generating Functions
拓展二项式定理
e.g. 生成函数解决 r 重组合问题
 更常规的例子是 r 可重复组合/r 个相同的放入 n 个不同的
更常规的例子是 r 可重复组合/r 个相同的放入 n 个不同的

Relations
基本概念
如果 A B 是两个集合 那么从 A 到 B 的关系就是 的一个子集 R 当然 我们有的时候更关注集合 A 到她本身的关系
所以说集合 A 上的关系就是集合 A 本身笛卡尔积的一个子集
所以这个关系可以用一个 的一个矩阵来表示
这个矩阵可以进行乘方以及转置
Properties
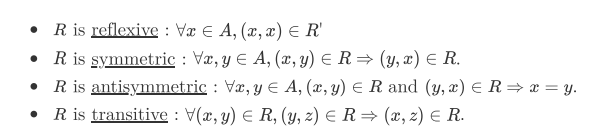 同时 一个矩阵可以被转化成特定的图 用来表示该关系
**The relation R on set A is transitive if and only of $R^{n}\subset R$**
同时 一个矩阵可以被转化成特定的图 用来表示该关系
**The relation R on set A is transitive if and only of $R^{n}\subset R$**
Inverse
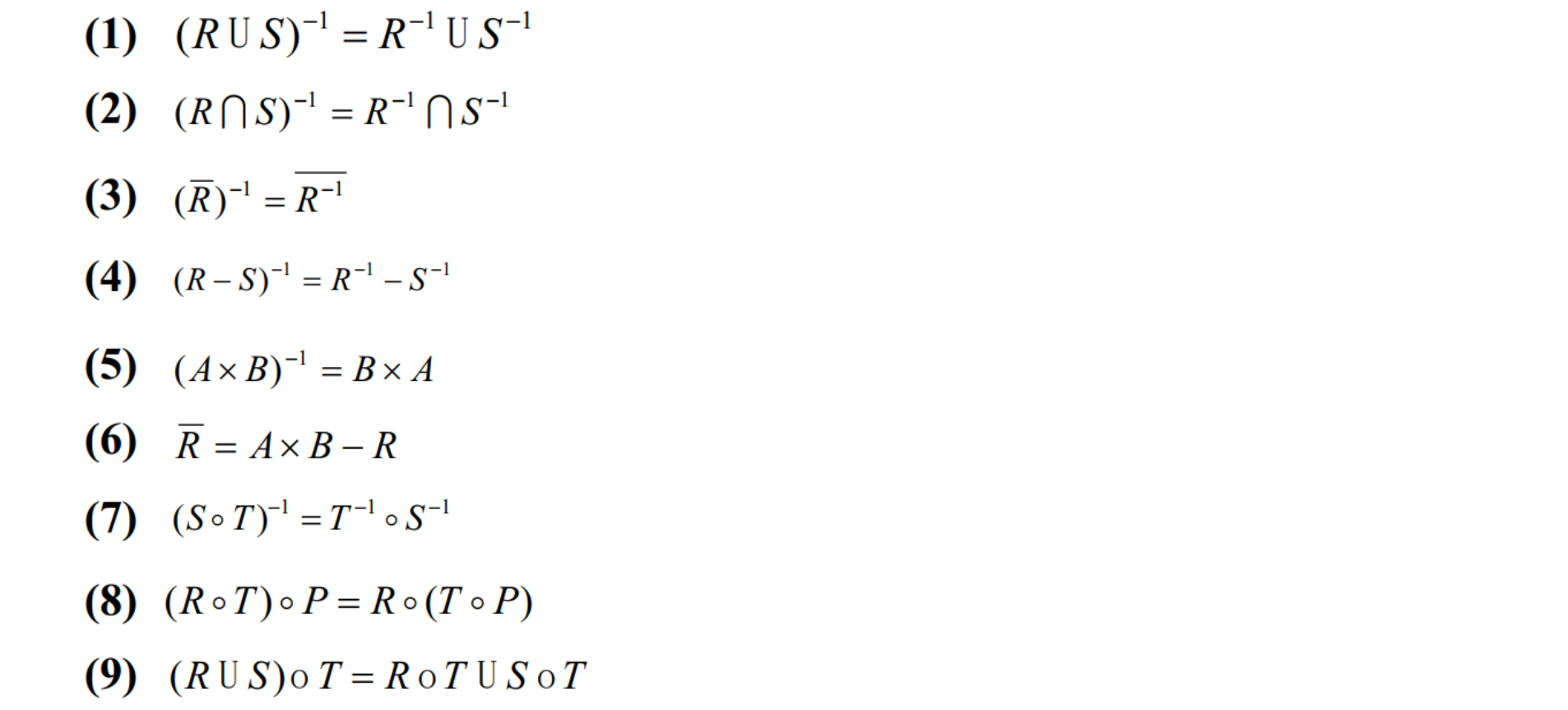
e.g. 关系计数问题
闭包
构造自反闭包:合并上所有对角线为 1 的
构造 symmetric 闭包:并上矩阵本身的转置
构造传递闭包 即 或者使用Warshall算法进行构造 也是进行 n 次 按照字母顺序来看节点 每次增加一个内部节点的可选择项(a,b,c……)然后每次在矩阵中添加上通过这些内部节点可以连通的路径
对于多种闭包的组合
先对称再传递再自反
等价关系 等价类
同时自反 对称 以及传递
对于任意一个元素[a] 所有与他具有等价关系的元素构成一个等价类 不同等价类之间是没有交集的
Partition
A collection of subsets of
偏序关系
reflexive + antisymmetric + transitive
[[9 Relation]]
well-ordered
every nonempty subset of ha a least element
proof
字典序
全序集
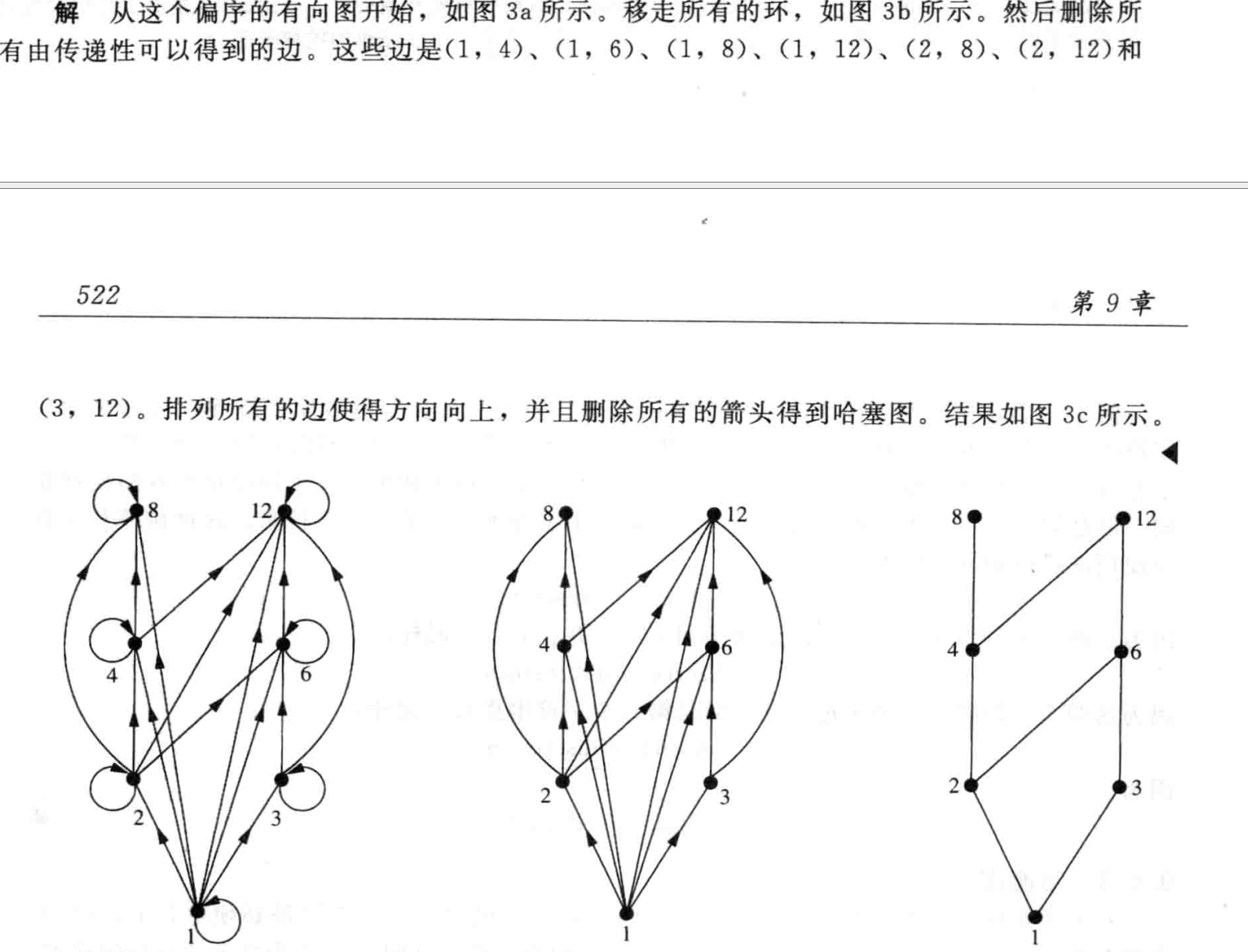
哈塞图
e.g. 整除关系 去掉自反 去掉传递(他们是必须存在的 所以无需额外表示) 去掉箭头
极大元 极小元 maximal and minimal
最大元 最小元 greatest and least (only one, maybe doesn’t exist)
上界 下界 最小上界 最大下界(注意!上下界可以包含该元素子集本身)
格
每一对元素(子集)都存在最小上界和最大下界 一般左右两条竖线之间的元素有一对交叉线的就不是格了
如何找到最小上界和最大下界(当元素是集合或者一个数时)
e.g. (A, C)其中 A 是元素 C 是一个集合
最小上界
最大下界
图
握手定理:所有顶点的度数之和为边数量的两倍
奇度顶点的个数一定为偶数
有向图中入度等于出度等于边的总数
automorphism:自同构,顶点和边的关系仍然一样
n-Cubes
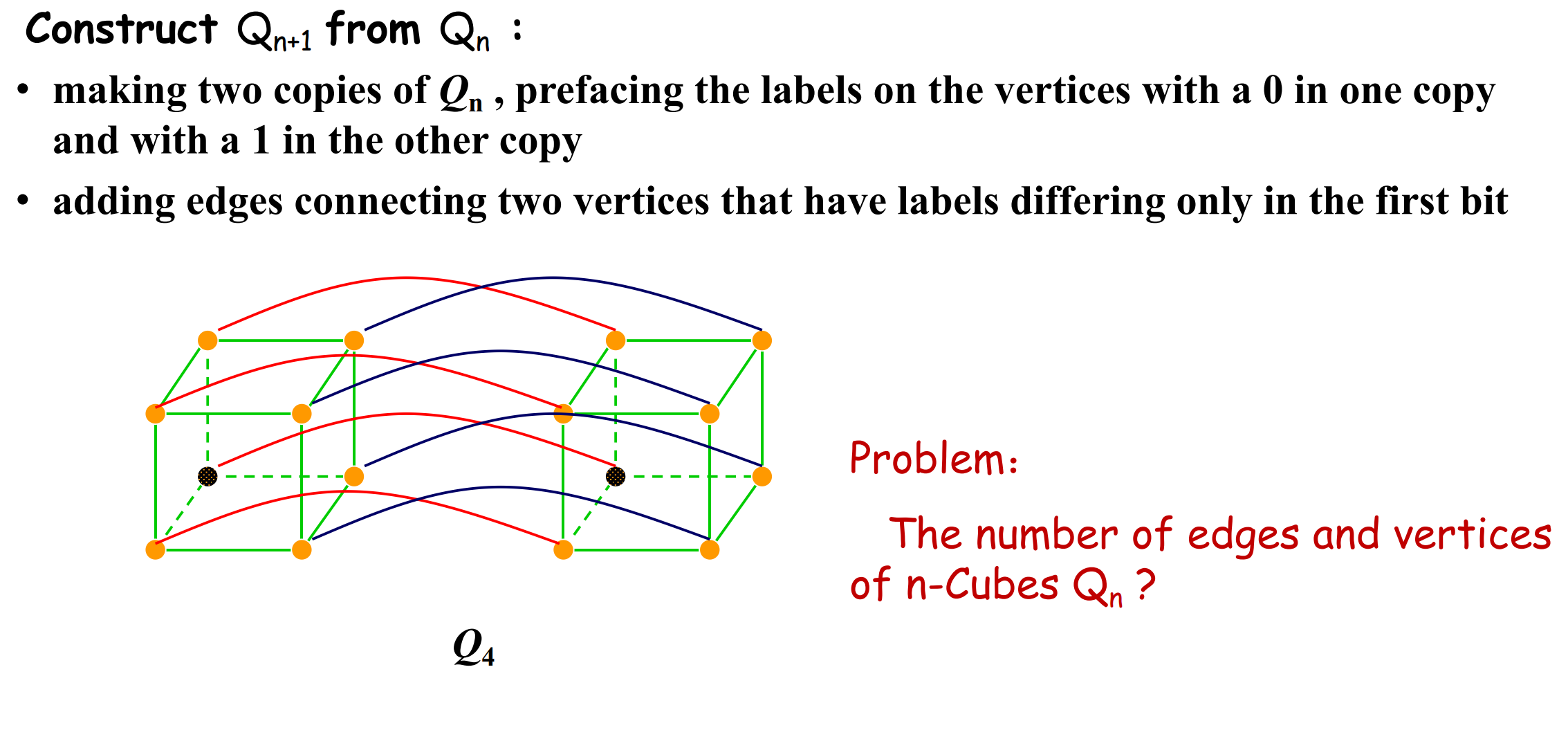 递推关系:$Q_{n}$有多少条边 多少个顶点 边的递推关系是什么 如何解出来
递推关系:$Q_{n}$有多少条边 多少个顶点 边的递推关系是什么 如何解出来
Bipartite Graph
 如何判断:染成两种颜色 相邻的节点不能被染成同样的颜色
如何判断:染成两种颜色 相邻的节点不能被染成同样的颜色
 或者:不可能通过遍历奇数条不同的边,从某个顶点出发又回到该顶点。
或者:不可能通过遍历奇数条不同的边,从某个顶点出发又回到该顶点。
匹配
- 匹配 M:它是边集合 E 的子集,满足没有两条边有共同的顶点,即对于不同的边{s, t}和{u, v},顶点 s, t, u, v 是不同的。
- 最大匹配:拥有最大边数的匹配
- 完全匹配:所有都被包括在匹配M中边的顶点中
- 霍尔婚配定理:对于的所有子集:
Isomorphism
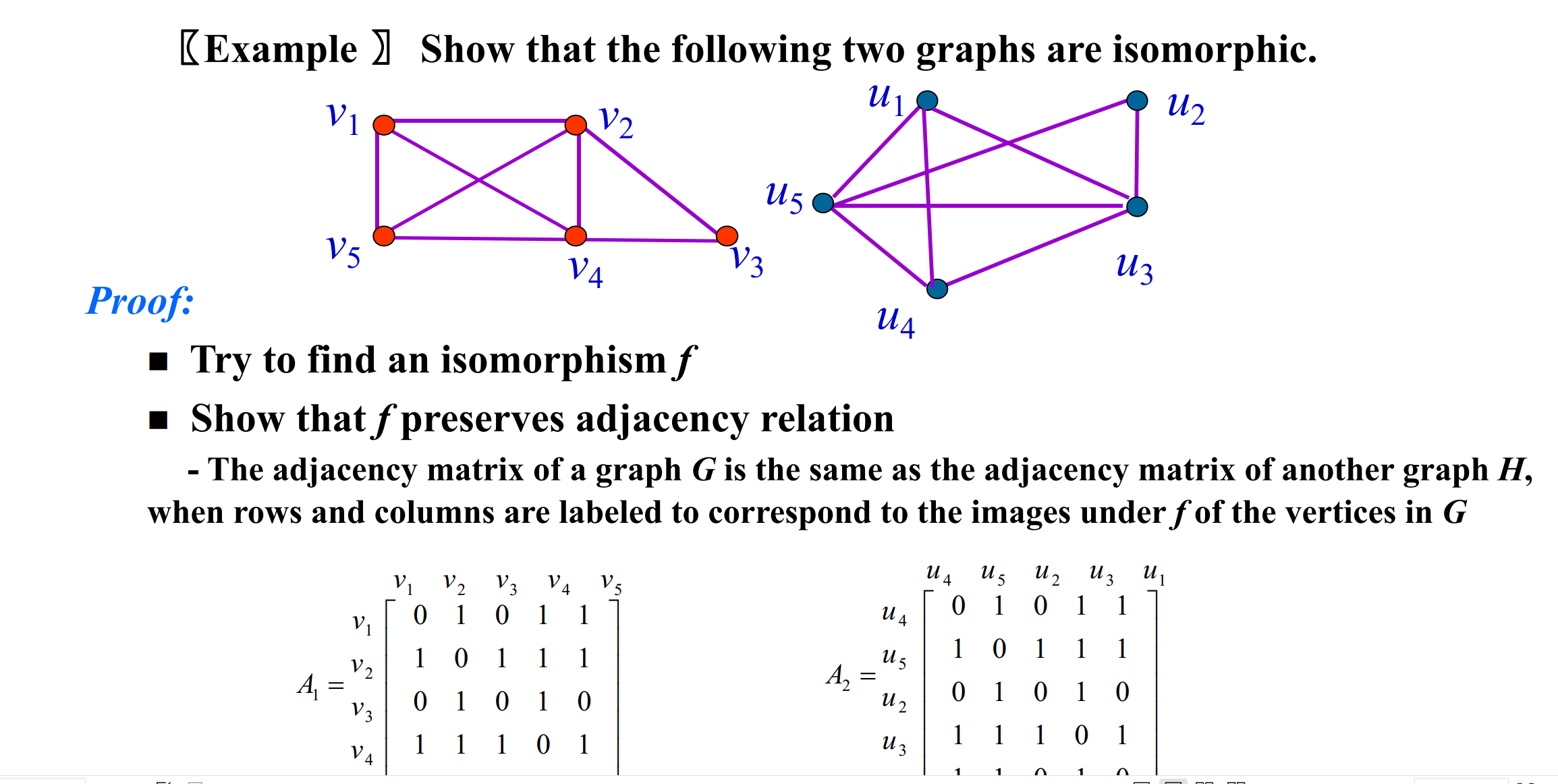 可以有$n!$个对应函数(n 个节点对应 n 个节点) 可以把邻接矩阵写出来 然后调换节点的位置->构造出了一个同构图
可以利用顶点的度(数量、入度、出度) 悬挂顶点 有 loop 的顶点 简单回路的长度 来否定图是同构的
可以有$n!$个对应函数(n 个节点对应 n 个节点) 可以把邻接矩阵写出来 然后调换节点的位置->构造出了一个同构图
可以利用顶点的度(数量、入度、出度) 悬挂顶点 有 loop 的顶点 简单回路的长度 来否定图是同构的
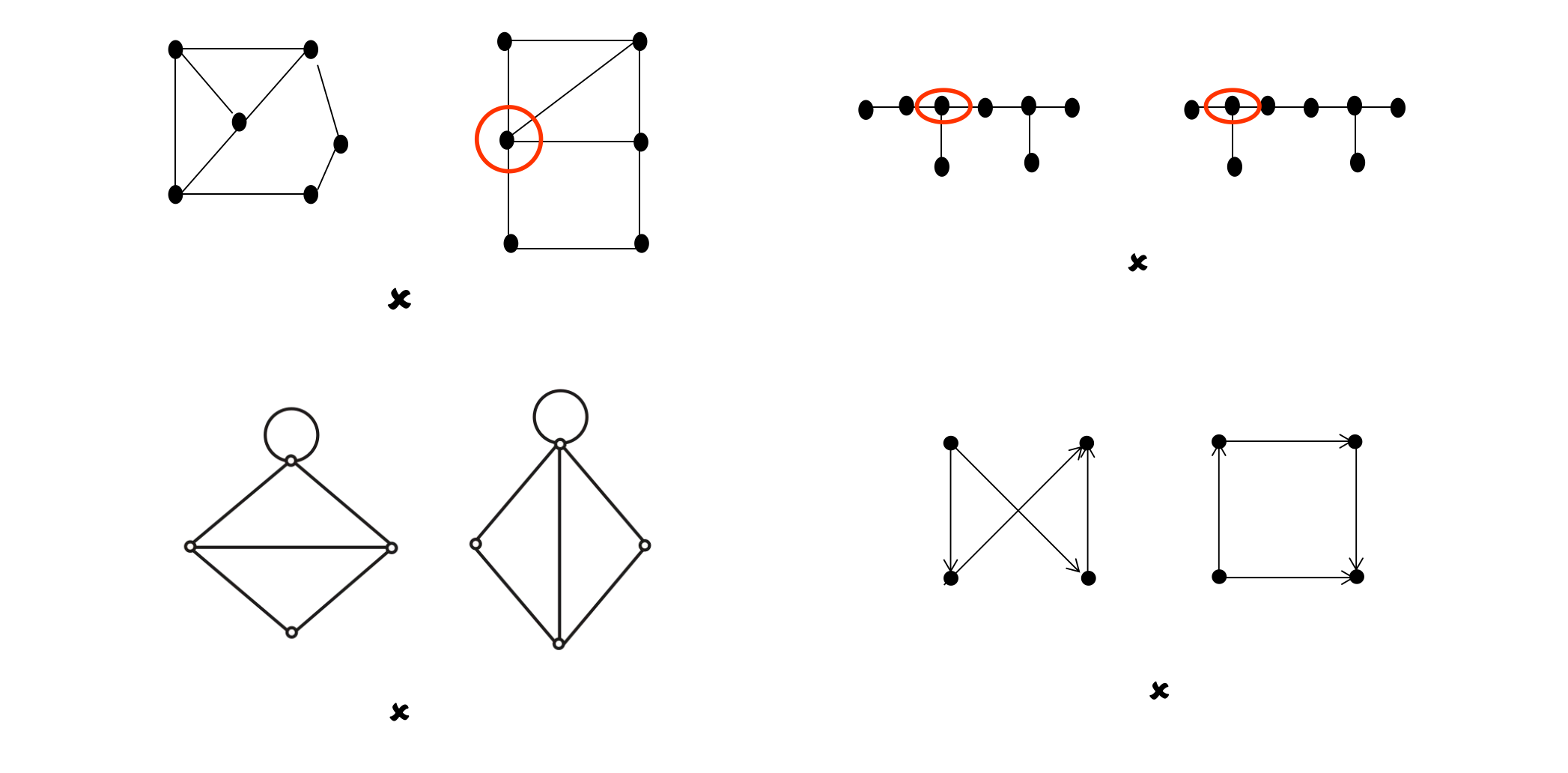
e.g.四个顶点的图 所有的不同构的生成子图
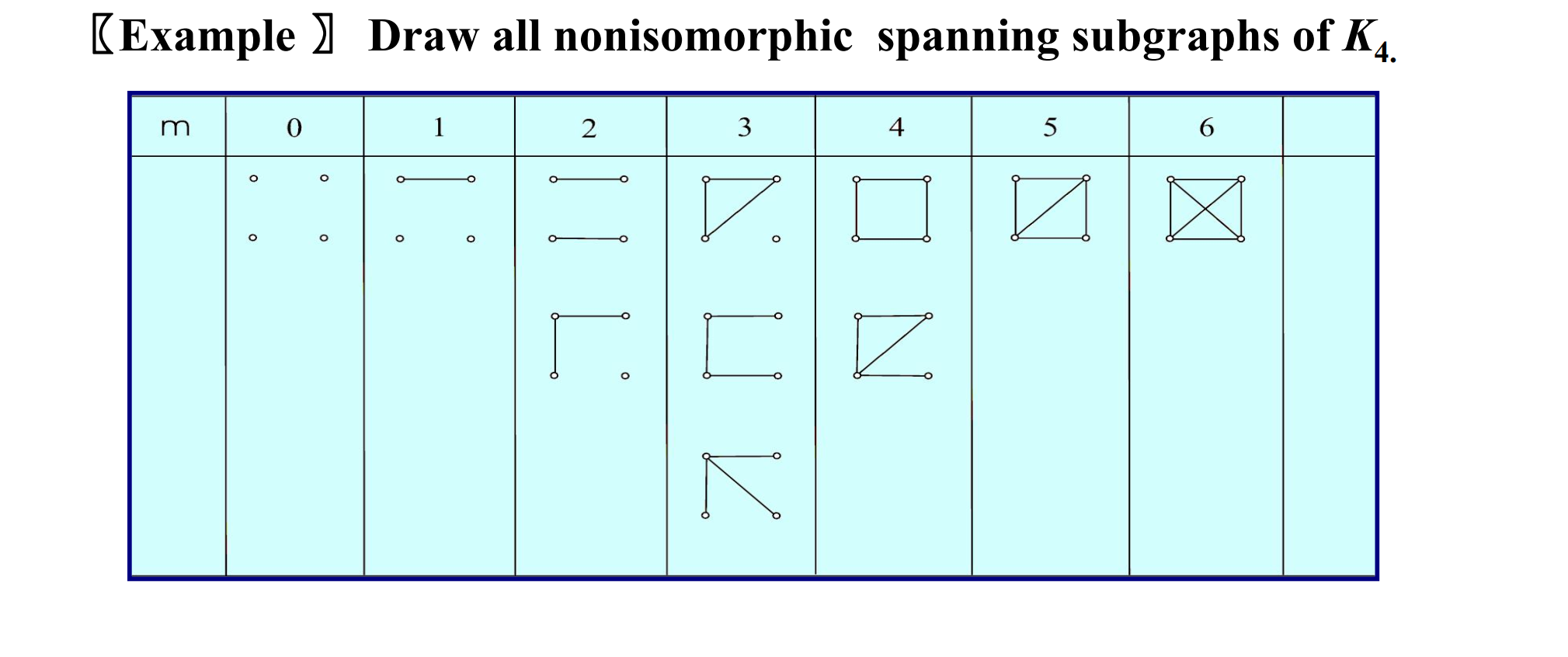
Counting Paths between Vertices 可达性
可达性矩阵也可用于
- 找到两个顶点间最短路径的长度
- 判断图是否连通
平面图 planer graph
欧拉公式(必要条件)
图 G 有 k 个联通分量 e 个边 v 个顶点 r 是平面图的区域数
推论 三种判断方法
如果 G 是连通平面简单图,那么 G 中存在一个度 ≤5 的顶点
如果平面简单连通图:没有长度为 3 的环
Homeopathic graph
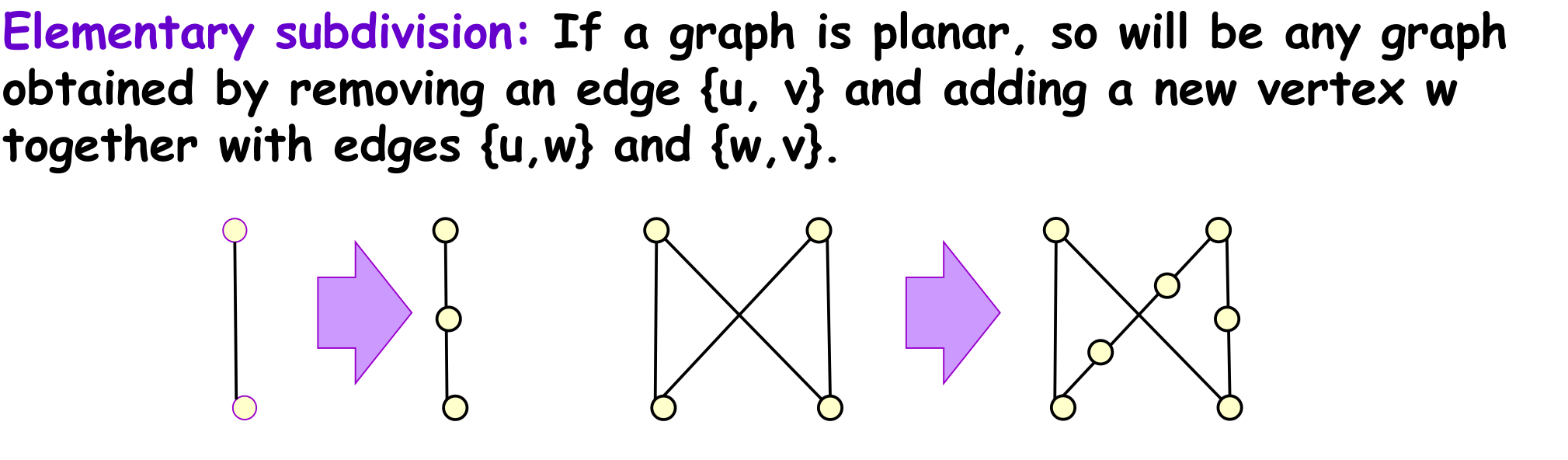 在平面图的基础上为某些边添加一个顶点
在平面图的基础上为某些边添加一个顶点
排除平面图的方法

Graph Coloring
dual graph
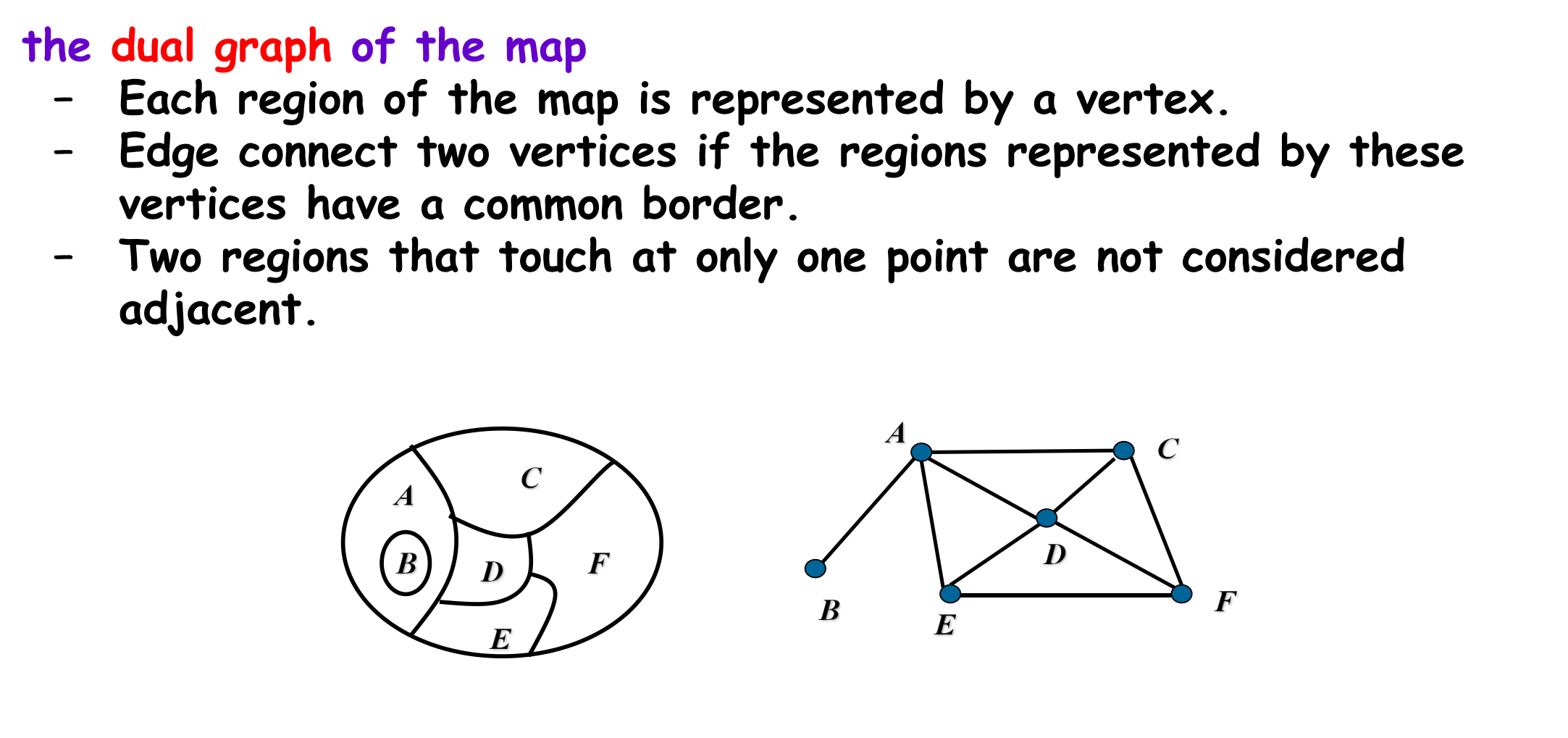 region -> vertex adjacency of region -> edge
region -> vertex adjacency of region -> edge
Chromatic number of a graph
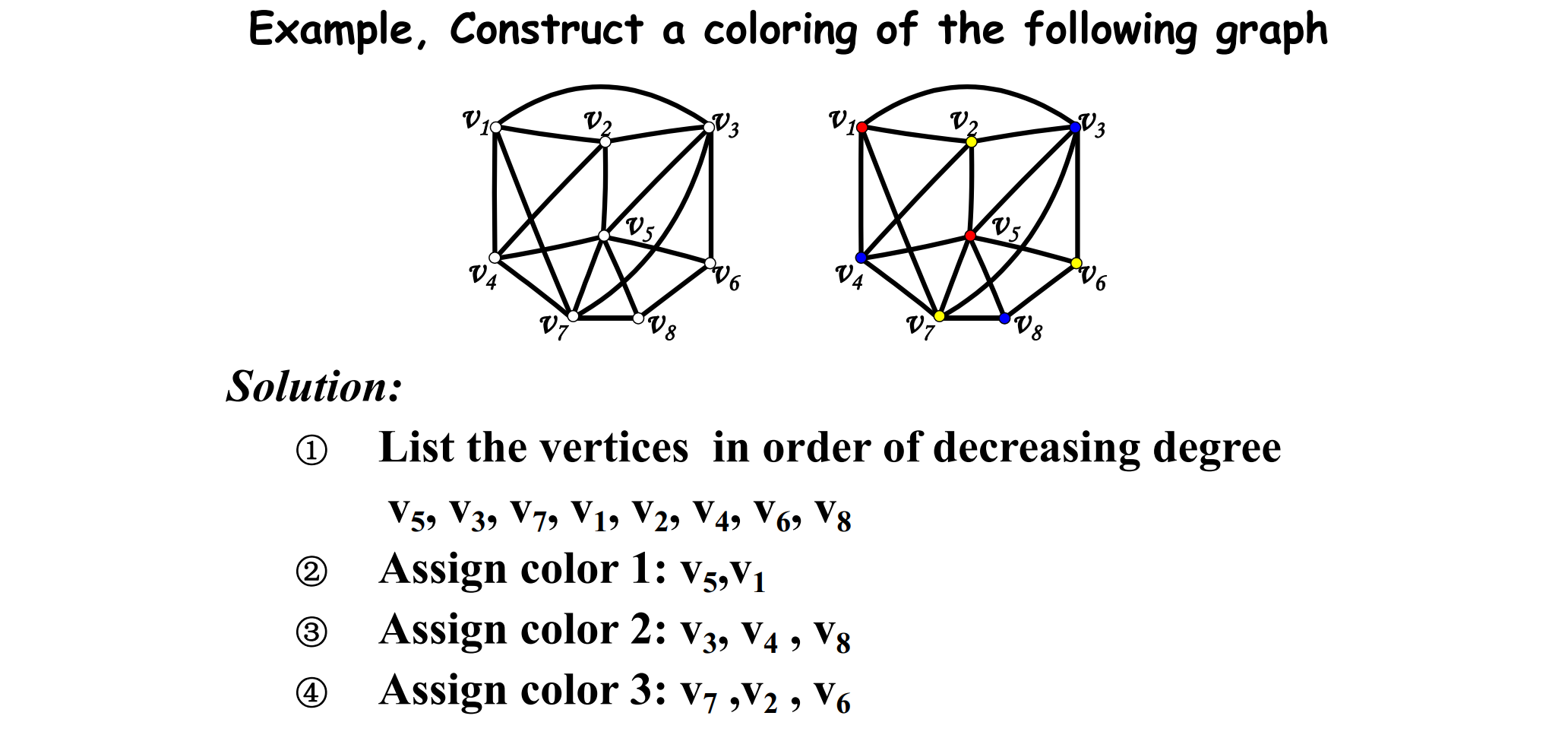 1 按照递减的顺序把顶点的度排序
2 按照从左到右 不相邻的着同一种颜色
3 如此循环
**a planer graph's chromatic number is not greater than four**
1 按照递减的顺序把顶点的度排序
2 按照从左到右 不相邻的着同一种颜色
3 如此循环
**a planer graph's chromatic number is not greater than four**
e.g.四个顶点的图 所有的不同构的生成子图

割点/割边 (重要的点和边)
删掉以后产生了不连通的子图
Vertex Cut
点割集
删除这个集合中的点 得到的删点子图一定是不连通的
不是完全图的连通图一定存在点割集
点割集中最小的顶点数记作 特殊地,对于完全图,因为不存在点割集。所以定义他的 即删除到只剩一个顶点
类似地 边割集
有向图的连通性
强连通/弱联通
数不同顶点之间边的数量
r 代表通过 r 条边可以互相联通
欧拉回路
全部顶点都是偶数 degree
找欧拉回路
用 DFS 不断寻找并添加 最终构造成一条完整的回路
欧拉道路
有且只有两个顶点有奇数 degree 起点和终点就是这两个顶点
有向图中的欧拉回路与欧拉道路

一笔画
2k 个奇数度顶点 至少需要 k 笔画
Hamilton
Path
visit every vertices exactly once
(is a simple path, Hamilton path 不一定是 Eular Path——可能不经过某些边 反之也不一定——可能重复经过某些顶点)
Circuit
visit every vertices excatly once except the first vertex

 减少判断的方法
1 有度为一的图不可能
2 度为二的顶点连接的两个边一定被包含在回路中
3 多个度的时候 除了被用过的两条边 其他的都可以不考虑
减少判断的方法
1 有度为一的图不可能
2 度为二的顶点连接的两个边一定被包含在回路中
3 多个度的时候 除了被用过的两条边 其他的都可以不考虑
最短
Tree
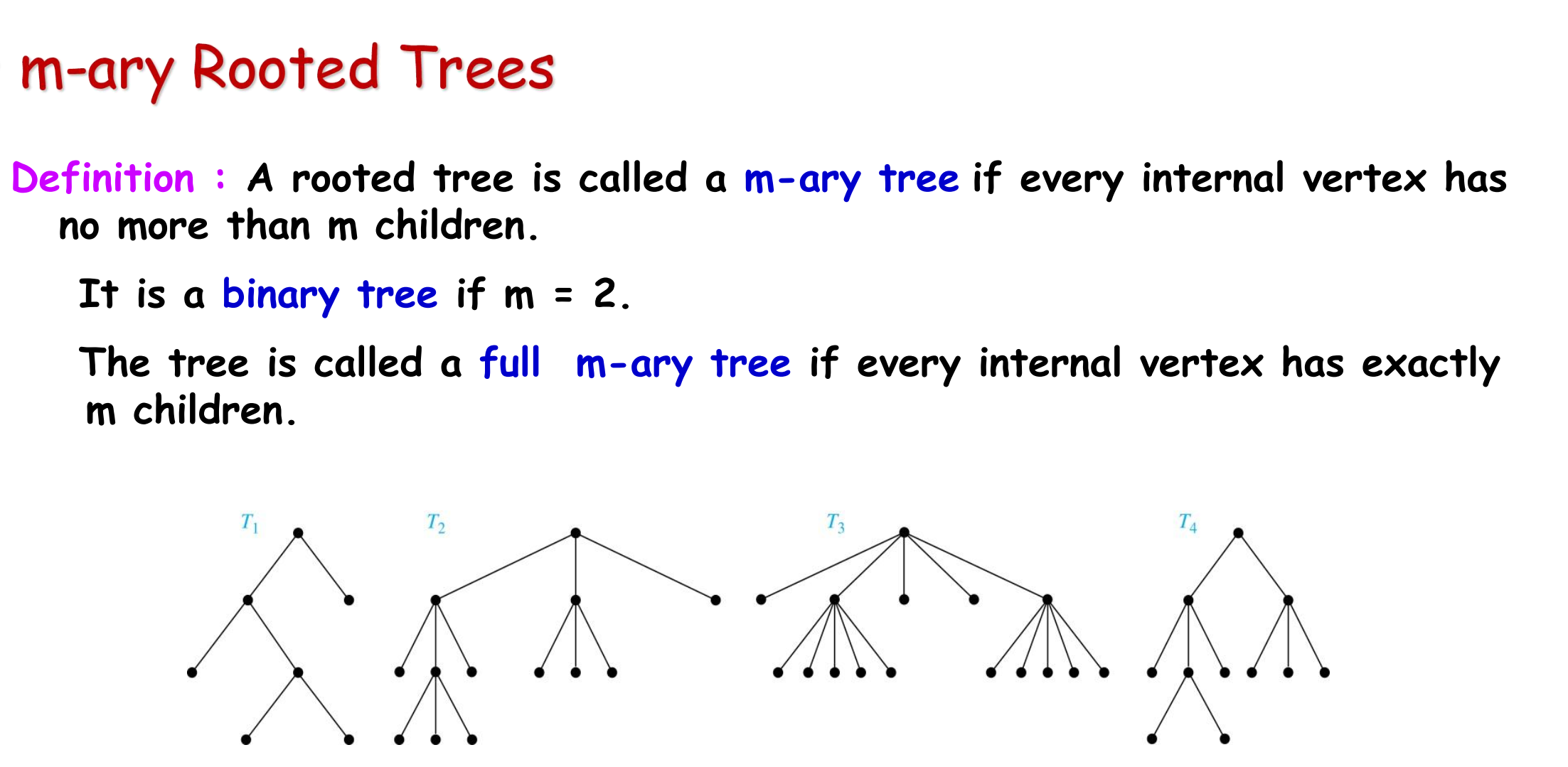
siblings, internal vertex, leaf, subtree, root
2-ary rooted tree -> binary tree
Properties of tree
1 n nodes -> n - 1 edges
e.g. number of no isomorphic unrooted/rooted trees
connected + no circuits —> tree
可以先找到unrooted的个数 再选择不同的根节点 也可以直接定一个根节点根据度数枚举
e.g. how many leaves in a graph with m 2-degree, n 3-degree vertices…
<img src="9ca104ff/Pasted image 20240604090544.png"/>
设度为n的顶点有x个 列出边和顶点个数的方程
every tree is bipartite and have chromatic number 2 and every edge is articular edge
balanced
all leaves are in level h or h - 1
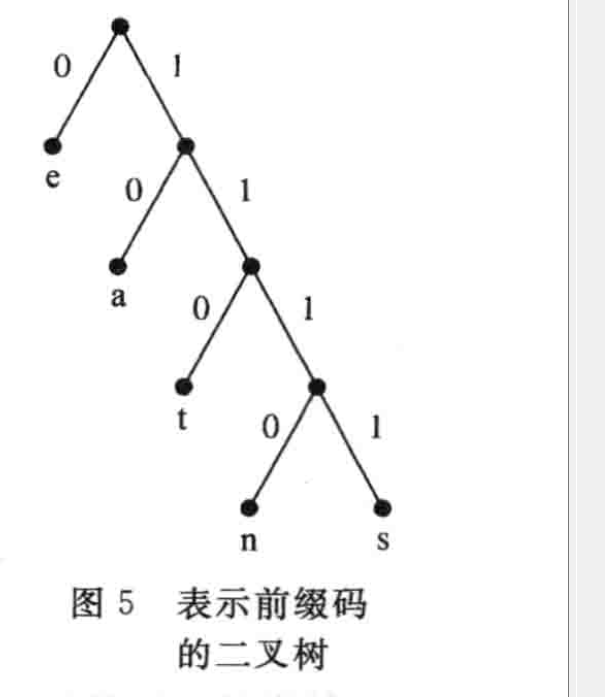
前缀码 Prefix Code

 可以用一个二叉树定义一种前缀码的编码规则 进行编码和解码
可以用一个二叉树定义一种前缀码的编码规则 进行编码和解码
哈夫曼编码
 初始化全部为一个根的森林
初始化全部为一个根的森林
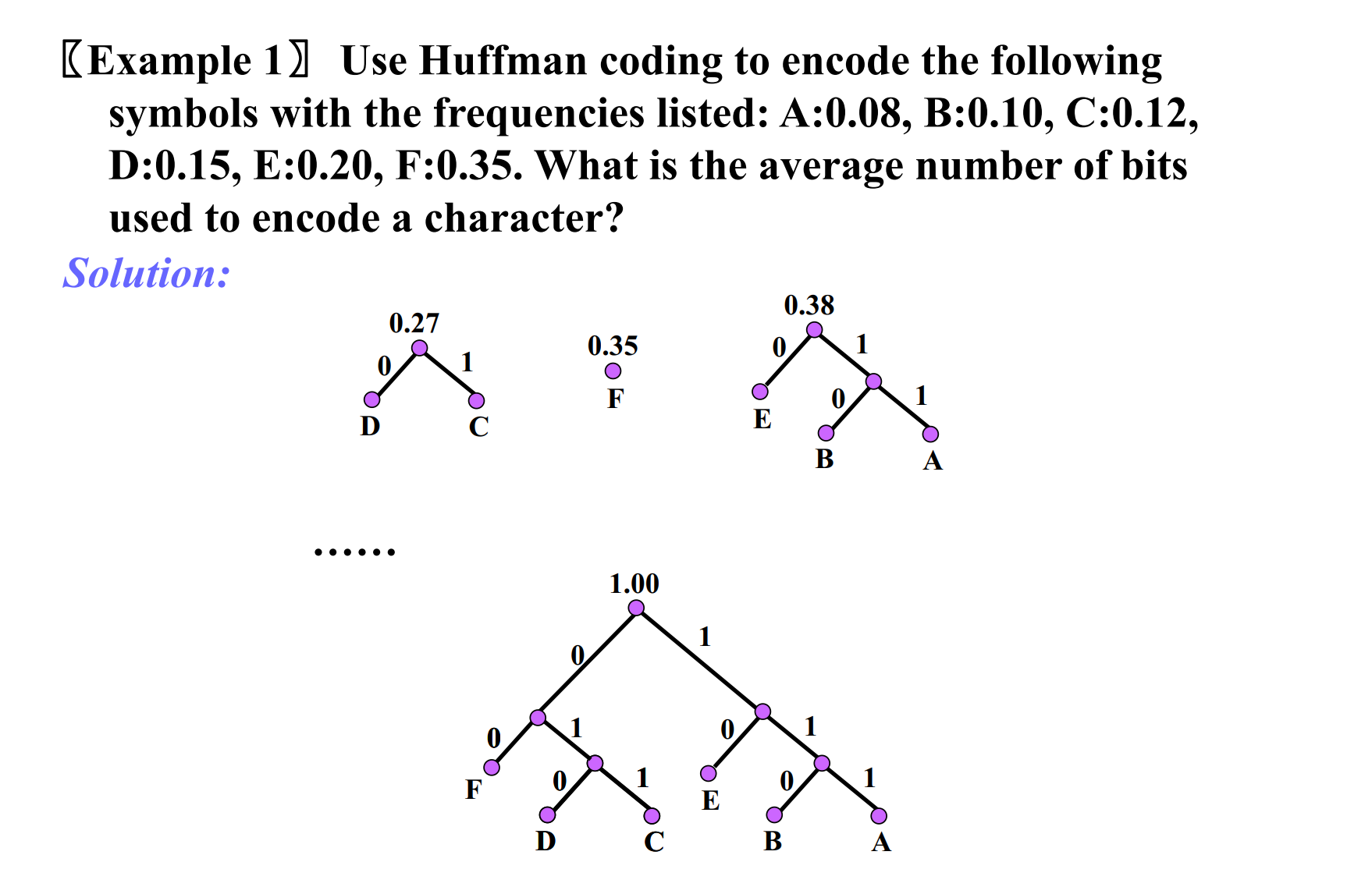 始终选择权重最小的两个根合并为一个新的树(创建一个新的根-权重等于他们之和)(权重相对小的在右子树)
直到形成一个完整的树 即为编码方法(可以自底向上或者自顶向下都可以)
始终选择权重最小的两个根合并为一个新的树(创建一个新的根-权重等于他们之和)(权重相对小的在右子树)
直到形成一个完整的树 即为编码方法(可以自底向上或者自顶向下都可以)

e.g. average bits used
频率乘上该字母在树中编码对应的bit位数
Spanning Tree
a subgraph which contains every vertices of a tree
不唯一
简单图是连通的 当且仅当 他有一个生成树
minimal spanning tree
Prim
- 重复以下步骤直到最小生成树包含图中的所有顶点:
- 从未加入最小生成树的顶点集合中,选择一个顶点 u,使得 key[u]最小且尚未加入最小生成树。(有点类似 Dijkstra 算法:最小未知/未加入的边)
- 将顶点 u 加入最小生成树集合 MST[]。
- 更新与顶点 u 相邻的顶点 v 的 key[]值,如果边(u, v)的权值小于 key[v],则将 key[v]更新为边(u, v)的权值,并将 parent[v]设置为 u。
Kruskal
- 将图中的所有边按照权值从小到大进行排序。(使用最小堆)
- 依次选择权值最小的边,如果该边连接的两个顶点不在同一个连通分量中(使用并查集),则将该边加入最小生成树,并将这两个顶点合并到同一个连通分量中。
- 重复上述步骤,直到最小生成树包含图中的所有顶点。
DFS
1 | void DFS(Vector V) { |
回溯 backtracking
e.g. 图着色
- 对于每一个节点,先选择可选列表(排除邻接他的颜色)中的第一个可选颜色
- 继续 DFS
- 如果有一个节点无可选颜色 就回溯直到可选列表有第二个颜色的
- 继续 DFS
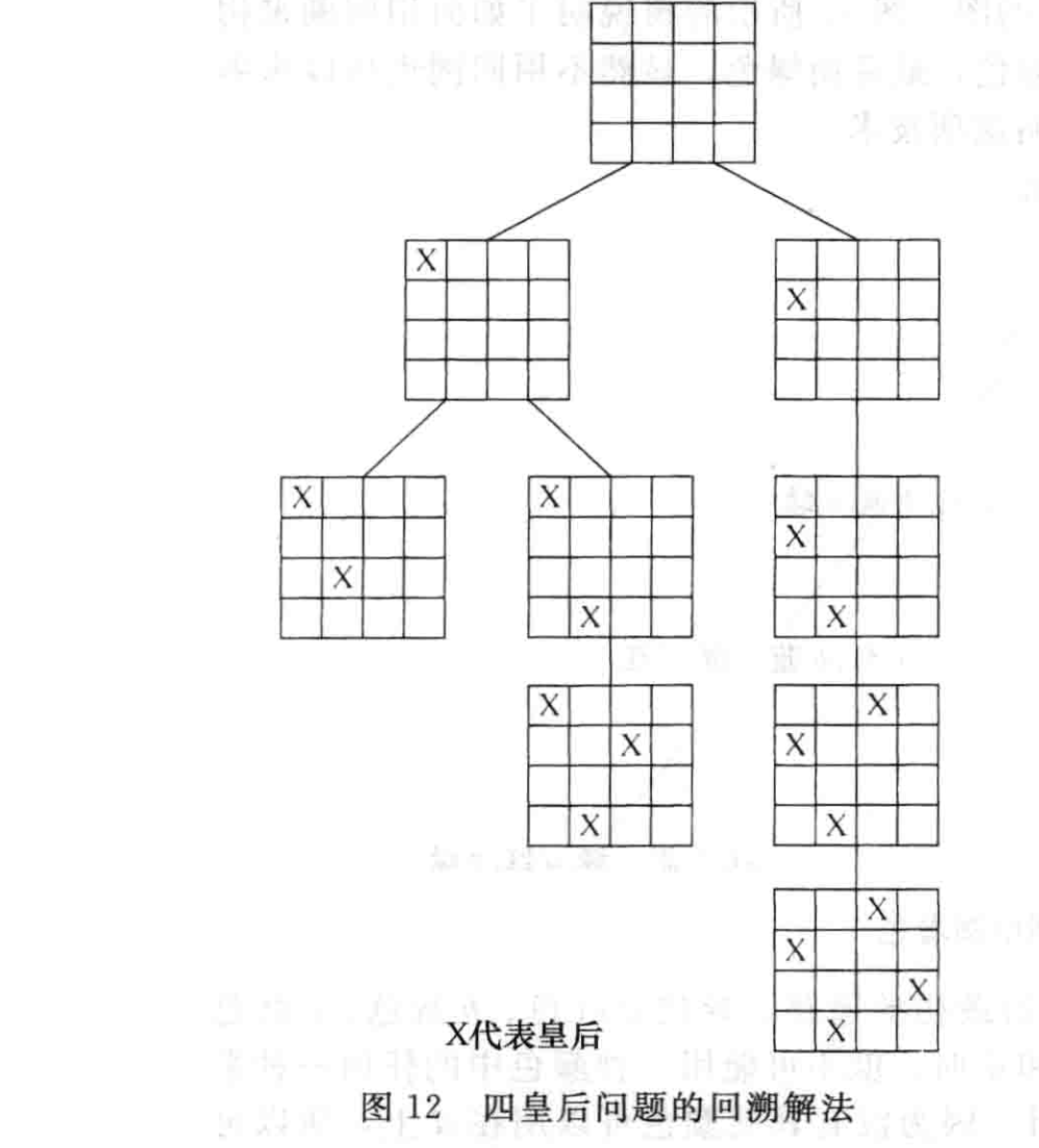
e.g. N 皇后
- 尝试放置,如果不行就回溯
e.g. 子集之和
- 尝试添加集合中的元素
- 如果比规定的元素之和要大 回溯 比规定的小 就暂时加入并且继续深入
BFS
(无权图的最短路径)
设置一个队列 先把源头节点入队列 然后 while 队列不为空 deQueue 一个节点 对于该节点所指向的所有节点,判断长度是否为无穷(之前没来) 设置其长度为 dequeue 节点长度+1 并且把它加入队列 时间复杂度








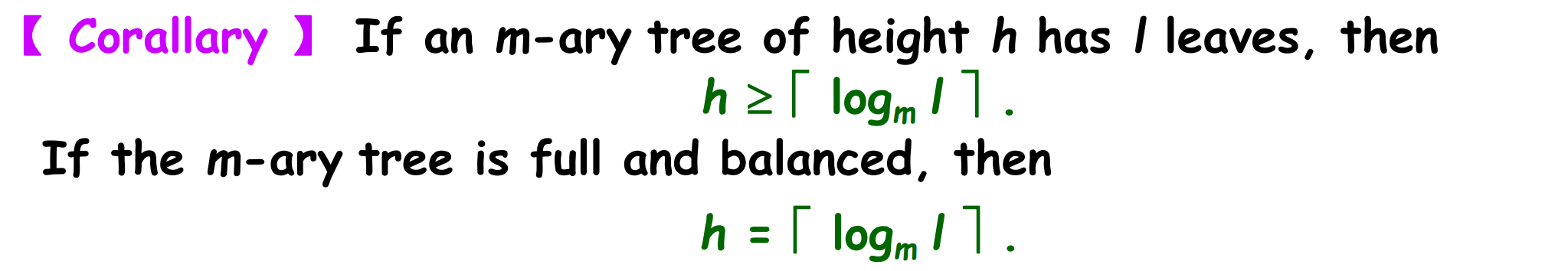



![[CTF实战]QQ盗号网站SQL注入攻击](https://s2.loli.net/2024/07/15/kdInMjAyZSuUBb7.png)
![[课程笔记]2024春夏 ZJU 数据结构基础](https://s2.loli.net/2024/07/15/tZBwHEjfqLKs45x.png)
![[misc]网站搭建中使用的python脚本和HTML前端代码](https://s2.loli.net/2024/07/15/eM2UuLr5t37XmF9.png)
![[CS学习]计算机网络](https://s2.loli.net/2024/07/15/3gzkTo129CQZXKP.png)
![[CTF技术]SQL注入攻击](https://s2.loli.net/2024/07/14/AJYsj9Mu2VKmHnz.png)